Unlocking the Magic of Tangent Half-Angle Substitution: A Journey into Trigonometric Elegance

Image 1 - visual representation

Since math was one of my interests, I often pondered and researched it during my leisure time. As usual, I received one challenging question from Mr. Betancourt, a math teacher at ASF, which opened up a path for me to learn about a beautiful method of substitution: the Tangent Half-angle substitution.

The journey to learning the Tangent Half-Angle substitution all started with one normal calculus question:

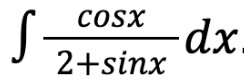
In this case, this problem could be simply solved by using the substitution method—substituting

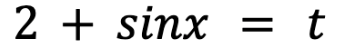
where

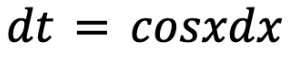
and the question simply turns into

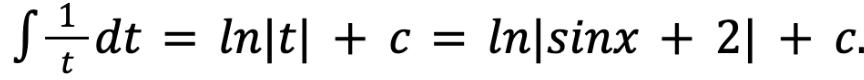
Yet, Mr. Betancourt gave the problem a little twist—which looked like a small modification on the surface, but completely changed the solution for it:

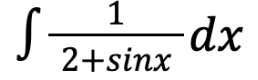
While it seemed like a normal integral problem as the previous one, the method that was used in the previous problem could not be applied since the numerator was changed from cosx to 1, making the ordinary substitution method impossible. Thus there needed to be another way of substituting in order to solve this problem. While having numerous attempts at substituting, one idea arose from the midst—it was the tangent. Compared to other trigonometry values such as sinx or cosx, tangent had a unique property also known as the sum angle formula of the tangent which is

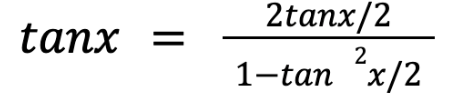
This was a crucial motive when solving this problem since this allowed representing not only tangent but also other trigonometry values as

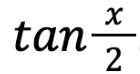
Thus, starting with this motive, I tried a substitution where I let

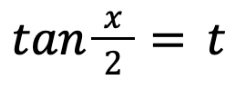
in this problem. Alas, all the trigonometry values could be changed into a form of t where

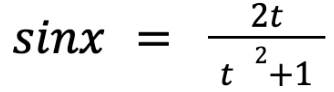
and

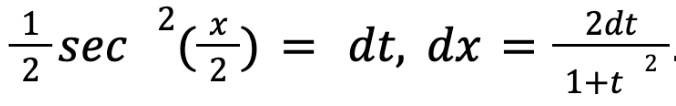
This allowed the initial question to change into the form of

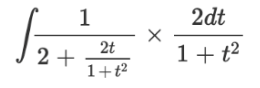
substituting sinx as

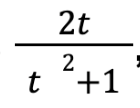
which could be simplified as

at this moment, the problem is almost complete. Lastly, to solve this equation there needs to be a little trick regarding the property of trigonometry—using the property that

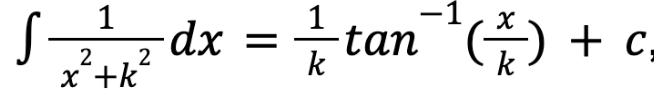
the integral could be modified as

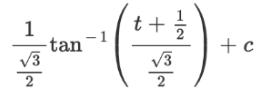
thus getting the answer

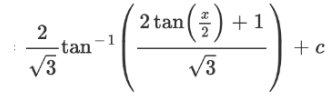
Overall, while by the initial glimpse, the tangent half-angle seems completely irrelevant to the problem, the tangent’s unique characteristic of its angle sum property allows this beautiful solution. Hope you enjoyed it as much as I did!